Metric Functions

A metric function is a function that takes a scale as input and returns a calculated value. As mentioned in Basic Concepts, it returns a Python dict with the metric name as the key, and the metric value as the value.

The currently defined metrics all estimate the consonance or dissonance of a scale.

sum_p_q()

pytuning.metrics.sum_p_q(scale)

Calculate a metric for a scale

Parameters:scale – The scale. Returns:A dict with the metric value.

This is an estimate of scale consonance. It is derived from summing the numerators and denominators of the scale degrees.

Smaller values are more consonant.

Note that this metric looks at the degrees of the scale, so it is somewhat tonic-focused. The similar metric sum_p_q_for_all_intervals() is similar, but it sums the numerator and denominator values for all distinct intervals within the scale.

While the metric is numerically defined for ratios expressed as irrational or transcendental numbers, it is really only meaningful for scales with just degrees (ratios expressed as rational numbers).

sum_p_q(create_pythagorean_scale())

yields:

{'sum_p_q': 3138}

sum_distinct_intervals()

pytuning.metrics.sum_distinct_intervals(scale)

Calculate a metric for a scale

Parameters:scale – The scale. Returns:A dict with the metric value.

This metric is an estimate of scale consonance. Numerically it is the number of distinct intervals within the scale (including all ratios and their inversions).

Smaller values are more consonant.

sum_distinct_intervals(create_pythagorean_scale())

yields:

{'sum_distinct_intervals': 22}

metric_3()

pytuning.metrics.metric_3(scale)

Calculate a metric for a scale

Parameters:scale – The scale. Returns:A dict with the metric value.

Metric 3 is an estimate of scale consonance. Given a ratio p/q, it is a heuristic given by the following:

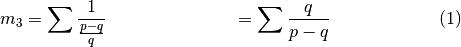
Smaller values are more consonant.

The summation takes place over all of the intervals in the scale. It does not form a set of distinct intervals.

sum_p_q_for_all_intervals()

pytuning.metrics.sum_p_q_for_all_intervals(scale)

Calculate a metric for a scale

Parameters:scale – The scale (i.e., a list of sympy.Rational values) Returns:The metric.

This metric is an estimate of scale consonance. It is formed by examining all unique intervals in the scale, and creating a numeric value based upon the summation of the numerators and denominators for all those intervals.

While the metric is numerically defined for ratios expressed as irrational or transcendental numbers, it is really only meaningful for scales with just degrees (ratios expressed as rational numbers).

Smaller values are more consonant.

sum_q_for_all_intervals()

pytuning.metrics.sum_q_for_all_intervals(scale)

Calculate a metric for a scale.

Parameters:scale – The scale (i.e., a list of Rational s) Returns:The metric.

Metric 5 is an estimate of scale consonance. It is summation of the denominators of the normalized distinct ratios of the scale.

Smaller values are more consonant.

All Metrics

There is also a function that calculates all defined metrics for a scale.

pytuning.metrics.all_metrics(scale)

Calculate all metrics for the scale

Parameters:scale – The scale (i.e., a list of Rational s) Returns:A dict containing all metrics.

As an example:

pythag = create_pythagorean_scale()
metrics = all_metrics(pythag)

will (currently) produce:

{
 'metric_3': 49.9049074891784,
 'sum_distinct_intervals': 22,
 'sum_p_q': 3138,
 'sum_p_q_for_all_intervals': 1092732,
 'sum_q_for_all_intervals': 452817
}

If new metrics are coded they should be added to the __all__ data member for inclusion here.