Number Theory¶
While this part of the package isn’t particularly fleshed out yet, there are a few number-theoretic functions for the analysis of scales.
Odd Limits¶
PyTuning contains functions for finding the odd Limit for both intervals and scales.
We can define and interval – say, 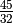 , and find its odd-limit
with the following:
, and find its odd-limit
with the following:
from pytuning.number_theory import odd_limit
interval = sp.Rational(45,32)
limit = odd_limit(interval)
which yields and answer of 45.
One can also find the odd limit of an entire scale with the find_odd_limit_for_scale()
function:
from pytuning.scales import create_euler_fokker_scale
from pytuning.number_theory import find_odd_limit_for_scale
scale = create_euler_fokker_scale([3,5],[3,1])
limit = find_odd_limit_for_scale(scale)
which yields 135. (Examining the scale:
![\left [ 1, \quad \frac{135}{128}, \quad \frac{9}{8}, \quad \frac{5}{4},
\quad \frac{45}{32}, \quad \frac{3}{2}, \quad \frac{27}{16},
\quad \frac{15}{8}, \quad 2\right ]](_images/math/e835d7625d8d24a0a7ccce7e033e5ee718608fff.png)
you will see that this is the largest odd number, and is found in the second degree.)
-
pytuning.number_theory.odd_limit(i)¶ Find the odd-limit of an interval.
Parameters: i – The interval (a sympy.Rational)Returns: The odd-limit for the interval.
-
pytuning.number_theory.find_odd_limit_for_scale(s)¶ Find the odd-limit of an interval.
Parameters: s – The scale (a list of sympy.Rationalvalues)Returns: The odd-limit for the scale.
Prime Limits¶
One can also compute prime limits for both scales and intervals. Extending the above example, one would assume that the Euler-Fokker scale would have a prime-limit of 5, since that’s the highest prime used in the generation, and in fact:
from pytuning.scales import create_euler_fokker_scale
from pytuning.number_theory import find_prime_limit_for_scale
scale = create_euler_fokker_scale([3,5],[3,1])
limit = find_prime_limit_for_scale(scale)
will return 5 as the limit.
-
pytuning.number_theory.prime_limit(i)¶ Find the prime-limit of an interval.
Parameters: i – The interval (a sympy.Rational)Returns: The prime-limit for the interval.
-
pytuning.number_theory.find_prime_limit_for_scale(s)¶ Find the prime-limit of an interval.
Parameters: s – The scale (a list of sympy.Rationalvalues)Returns: The prime-limit for the scale.
Prime Factorization of Degrees¶
PyTuning has functions for breaking a ratio down into prime factors, and the inverse of reassembling them.
-
pytuning.number_theory.prime_factor_ratio(r, return_as_vector=False)¶ Decompose a ratio (degree) to prime factors
Parameters: - r – The degree to factor (
sympy.Rational) - return_as_vector – If
True, return the factors as a vector (see below)
Returns: The factoring of the ratio
By default this function will return a
dict, with each key being a prime, and each value being the exponent of the factorization.As an example, the syntonic comma,
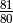 , can be factored:
, can be factored:r = syntonic_comma q = prime_factor_ratio(r) print(q) {2: -4, 3: 4, 5: -1}
which can be interpreted as:
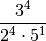
If
return_as_vectorisTrue, the function will return a tuple, with each position a successive prime. The above example yields:r = syntonic_comma q = prime_factor_ratio(r, return_as_vector=True) print(q) (-4, 4, -1)
Note that zeros will be included in the vector, thus:
r = sp.Rational(243,224) q = prime_factor_ratio(r, return_as_vector=True) print(q) (-5, 5, 0, -1) q = prime_factor_ratio(r) print(q) {2: -5, 3: 5, 7: -1}
- r – The degree to factor (
-
pytuning.number_theory.create_ratio_from_primes(factors)¶ Given a prime factorization of a ratio, reconstruct the ratio. This function in the inverse of
prime_factor_ratio().Parameters: factors – The factors. Can be a dictor atuple(seeprime_factor_ratiofor a discussion).Returns: The ratio ( sympyvalue).