Basic Concepts¶
PyTuning is purposefully designed to be as simple as possible, so that non-programmers (musicologists, musicians, etc.) can use it without too much difficulty: the data structures are relatively simple; there are currently no classes defined, instead opting for an imperative/procedural approach.
Regardless of how it is used (interactively or as a development library), the user should have a good understanding of some of the basic, foundational concepts the package uses.
Scales¶
A scale is, simply, a list of degrees. By convention the list is bookended
by the unison and the octave, with each degree given as a frequency ratio
relative to the root tone of the scale. The first degree is
always 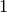 , the ratio of the first degree to the first degree. Most
commonly the last degree is
, the ratio of the first degree to the first degree. Most
commonly the last degree is 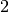 , as the octave is usually twice
the frequency of the root (although the package has some support for
non-standard “octaves”).
, as the octave is usually twice
the frequency of the root (although the package has some support for
non-standard “octaves”).
As an example, this is the standard 12-tone equal temperament scale (sometimes referred to as 12-TET, or 12-EDO, for Equal Division of the Octave).
![\left [ 1, \quad \sqrt[12]{2}, \quad \sqrt[6]{2}, \quad \sqrt[4]{2}, \quad \sqrt[3]{2}, \quad 2^{\frac{5}{12}}, \quad \sqrt{2},
\quad 2^{\frac{7}{12}}, \quad 2^{\frac{2}{3}}, \quad 2^{\frac{3}{4}}, \quad 2^{\frac{5}{6}}, \quad 2^{\frac{11}{12}}, \quad 2\right ]](_images/math/3561b502bdcc5a1adc4952cc413e9a2b8dab22e3.png)
A few things to note:
- As mentioned previously, the scale includes the unison and octave.
- Each scale degree is a SymPy number, so it is represented symbolically. Note that algebraic simplifications are performed by default.
- Even though the length of this list of 13, it is considered a 12 note scale, because the unison and the octave is in actuality the same note. Many of the functions in this package ask one to choose the number of notes or degrees to be used in this function. For these you should follow this convention.
(For those who are curious: the generation of scales is documented in Scale Creation, but the above scale was generated with the following code:
from pytuning.scales import create_edo_scale
edo_12_scale = create_edo_scale(12)
Simplified versions of most functions are provided in the interactive environment.)
Degrees¶
Scale degrees (which are expressed as frequency rations relative to the
tonic of the scale) are expressed in SymPy
values. In practical terms the Integer and Rational class will be
used the most, but SymPy is a full-featured package, and you may benefit
from having some familiarity with it.
An example of a few degrees:
import sympy as sp
unison = sp.Integer(1) # Normal unison
octave = sp.Integer(2) # Normal octave
perfect_fifth = sp.Rational(3,2) # As a rational number
minor_second_tet = sp.Integer(2) ** sp.Rational(1,12) # the 12th root of 2
# could also by sp.root(2,12)
lucy_L = sp.root(2,2*sp.pi) # Lucy scale Long step
Will yield the following:
![1 \\
2 \\
\frac{3}{2} \\
\sqrt[12]{2} \\
2^{\frac{1}{2 \pi}}](_images/math/b5b2001c04cbc3f5319c05735a7153a85f61fb7b.png)
SymPy manipulates all values analytically, but sometimes one needs a floating
approximation to a degree (for example, tuning a synthesizer usually needs
frequencies expressed as floating point numbers). For the evalf()
member function can be used:
print(unison.evalf())
1.00000000000000
print(octave.evalf())
2.00000000000000
print(perfect_fifth.evalf())
1.50000000000000
print(minor_second_tet.evalf())
1.05946309435930
print(lucy_L.evalf())
1.11663288009114
Modes¶
A mode is a selection of notes from a scale, and is itself a list of degrees (and therefore is also a scale). A mode can be produced from a scale by applying a mask to the scale. Again, the functions involved are documented elsewhere, but as example this is how we would produce the standard major scale (which in the context of this package would be referred to as a mode):
major_mask = (0,2,4,5,7,9,11,12)
major_mode = mask_scale(edo_12_scale, major_mask)
which produces the following scale:
![\left [ 1, \quad \sqrt[6]{2}, \quad \sqrt[3]{2}, \quad 2^{\frac{5}{12}},
\quad 2^{\frac{7}{12}}, \quad 2^{\frac{3}{4}}, \quad 2^{\frac{11}{12}},
\quad 2\right ]](_images/math/3ad9a0e617cf910e895ec5908d31bad28f2f60d4.png)
Mode Objects¶
Some functions in this package return a mode object. For
example, the find_best_modes() function will take a scale and find
a mode (or modes), based upon some consonance metric function.
Here is one such object, which is implemented as a Python dict.
{'mask': (0, 2, 3, 5, 7, 9, 10, 12),
'metric_3': 22.1402597402597,
'original_scale': [1,
256/243,
9/8,
32/27,
81/64,
4/3,
1024/729,
3/2,
128/81,
27/16,
16/9,
243/128,
2],
'scale': [1, 9/8, 32/27, 4/3, 3/2, 27/16, 16/9, 2],
'steps': [2, 1, 2, 2, 2, 1, 2],
'sum_distinct_intervals': 12,
'sum_p_q': 161,
'sum_p_q_for_all_intervals': 4374,
'sum_q_for_all_intervals': 1822}
The meaning of these keys:
original_scaleis the original scale which was input into the function. In this example is was a Pythagorean scale.scaleis the output scale of the functionmaskis the mask of the original scale that produces the outputstepsis similar to mask, but reported in a different format. Each entry in the steps list represents the number of degrees in the original scale between successive degrees in the returned scale. The standard major scale, for example, would be represented by![\left[ 2, 2, 1, 2, 2, 2, 1 \right]](_images/math/a06c8326bc615fd7e88aa4fc9bdc4b876b751d7b.png) .
.
In this example there are also other keys included. sum_distinct_intervals,
sum_p_q, sum_p_q_for_all_intervals, sum_q_for_all_intervals, and
metric_3 are the outputs of calculated metric functions. This particular mode,
for example, has a rating of 161 by the sum_p_q metric.
Metric functions are describe briefly below, and in more detail in Metric Functions.
Tuning Tables¶
Tuning Tables are a representation of a scale, usually a string (which can be written to a file), which can be understood by an external software package. As an example, to take a standard Pythagorean scale and produce a representation understood by Scala:
pythag_scale = create_pythagorean_scale()
scala_tuning_table = create_scala_tuning(pythag_scale, "Pythagorean Scale")
The variable scala_tuning_table now contains the following:
! Scale produced by pytuning. For tuning yoshimi or zynaddsubfx,
! only include the portion below the final '!'
!
Pythagorean Scale
12
!
256/243
9/8
32/27
81/64
4/3
1024/729
3/2
128/81
27/16
16/9
243/128
2/1
For many tuning tables one has to pin the scale to some reference
frequency. For this the convention of MIDI note number is employed. For
example, in the MIDI standard the note 69 is A 440 Hz, so by
specifying a reference of 69, the corresponding entry in the table
would be 400 Hz, and this would represent the root or tonic degree of
the scale.
Exporting the above scale in a Csound compatible format:
csound_tuning_table = create_csound_tuning(pythag_scale, reference_note=69)
yields the following:
f1 0 256 -2 8.14815 8.70117 9.16667 9.65706 10.31250 10.86420 11.60156 12.22222 \
13.05176 13.75000 14.48560 15.46875 16.29630 17.40234 18.33333 19.31413 \
20.62500 21.72840 23.20313 24.44444 26.10352 27.50000 28.97119 30.93750 \
32.59259 34.80469 36.66667 38.62826 41.25000 43.45679 46.40625 48.88889 \
52.20703 55.00000 57.94239 61.87500 65.18519 69.60938 73.33333 77.25652 \
82.50000 86.91358 92.81250 97.77778 104.41406 110.00000 115.88477 123.75000 \
130.37037 139.21875 146.66667 154.51303 165.00000 173.82716 185.62500 195.55556 \
208.82813 220.00000 231.76955 247.50000 260.74074 278.43750 293.33333 309.02606 \
330.00000 347.65432 371.25000 391.11111 417.65625 440.00000 463.53909 495.00000 \
521.48148 556.87500 586.66667 618.05213 660.00000 695.30864 742.50000 782.22222 \
835.31250 880.00000 927.07819 990.00000 1042.96296 1113.75000 1173.33333 1236.10425 \
1320.00000 1390.61728 1485.00000 1564.44444 1670.62500 1760.00000 1854.15638 1980.00000 \
2085.92593 2227.50000 2346.66667 2472.20850 2640.00000 2781.23457 2970.00000 3128.88889 \
3341.25000 3520.00000 3708.31276 3960.00000 4171.85185 4455.00000 4693.33333 4944.41701 \
5280.00000 5562.46914 5940.00000 6257.77778 6682.50000 7040.00000 7416.62551 7920.00000 \
8343.70370 8910.00000 9386.66667 9888.83402 10560.00000 11124.93827 11880.00000 12515.55556
This is a 128-entry table, mapping note number to absolute frequency. Csound’s
table opcode can be used to index into the table and play the appropriate
frequency, using something like the following:
inote init p4
iveloc init p5
ifreq table inote, 1
a1 oscil iveloc, ifreq, 2
outs a1, a1
(This assumes that p4 in the orchestra file contains MIDI note numbers, of course. If you use a different convention there are translation opcodes that can be used.)
Metric Functions¶
Metric Functions are functions that takes a scale as an input and returns
a numeric value calculated from that scale. It is used, for example, in
find_best_modes() to evaluate the consonance of a scale (find_best_modes()
uses a metric to evaluate the consonance of all possible modes of a scale and
returns the evaluation of those modes as a mode_object).
The return value of a metric function should be a dict with a unique string
identifier as the key and the metric as the value.
As an example, the following is one of the package-defined metrics:
As an example of use, the following:
pythag = create_pythagorean_scale()
metric = sum_p_q_for_all_intervals(pythag)
yields the following:
{'sum_p_q_for_all_intervals': 1092732}