Visualizations¶

PyTuning includes some visualizations for the analysis of scales, but this is not yet fleshed out.

The graphics are via Matplotlib, which is the de facto implementation of analytical graphics for python. There is also an optional dependency on Seaborn. Seaborn is good to include if you can – it makes the graphs better – but it’s a large package, owning to its dependencies (which include SciPy and Pandas; great packages, but extensive and large). If you have disk space to spare you may want to install it; otherwise you can get my with Matplotlib alone. On my system SciPy and Pandas weigh in at about 200 megabytes, not including any dependencies that they require. Matplotlib, on the other hand, is about 26 megabytes.

The Consonance Matrix¶

It’s nice to be able to get an intuitive feeling for the consonance or dissonance of a scale. For this, the consonance matrix is provided.

The consonance matrix forms an interval between every degree in the scale and applies a metric function to it. The default metric function just measures the denominator of the interval after any simplification it can undergo (and is really only meaningful for degrees which are expressed an integer ratios).

As an example, we can create a scale of the Euler-Fokker type:

scale = create_euler_fokker_scale([3,5],[2,1])

which is

$\left [ 1, \quad \frac{9}{8}, \quad \frac{5}{4}, \quad \frac{45}{32}, \quad \frac{3}{2}, \quad \frac{15}{8}, \quad 2\right ]$

Now, to create a consonance matrix:

from pytuning.visualizations import consonance_matrix
matrix = consonance_matrix(scale)

matrix now contains a matplotlib Figure. To write it as PNG:

matrix.savefig('consonance.png')

Which yields:

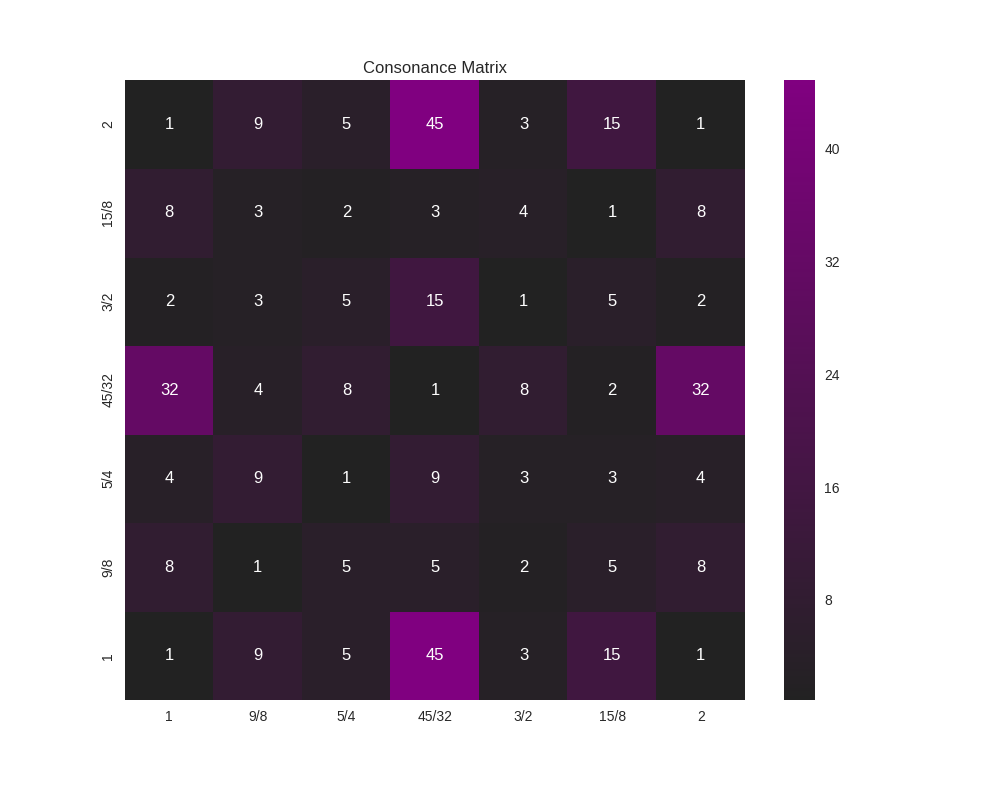
Because this function accepts an arbitrary metric, it can be used for any analysis performed on the intervals of a scale; it does not need to really be a measurement or estimate of consonance. As an example, let’s say that (for some reason) you’re interested in how far from unity each interval is:

def metric_unity(degree):
    normalized_degree = normalize_interval(degree)
    y = abs (1.0 - normalized_degree.evalf())
    return y

scale = create_euler_fokker_scale([3,5],[2,1])
matrix = consonance_matrix(scale, metric_function=metric_unity, title="Distance from Unity")

Our graph now looks like:

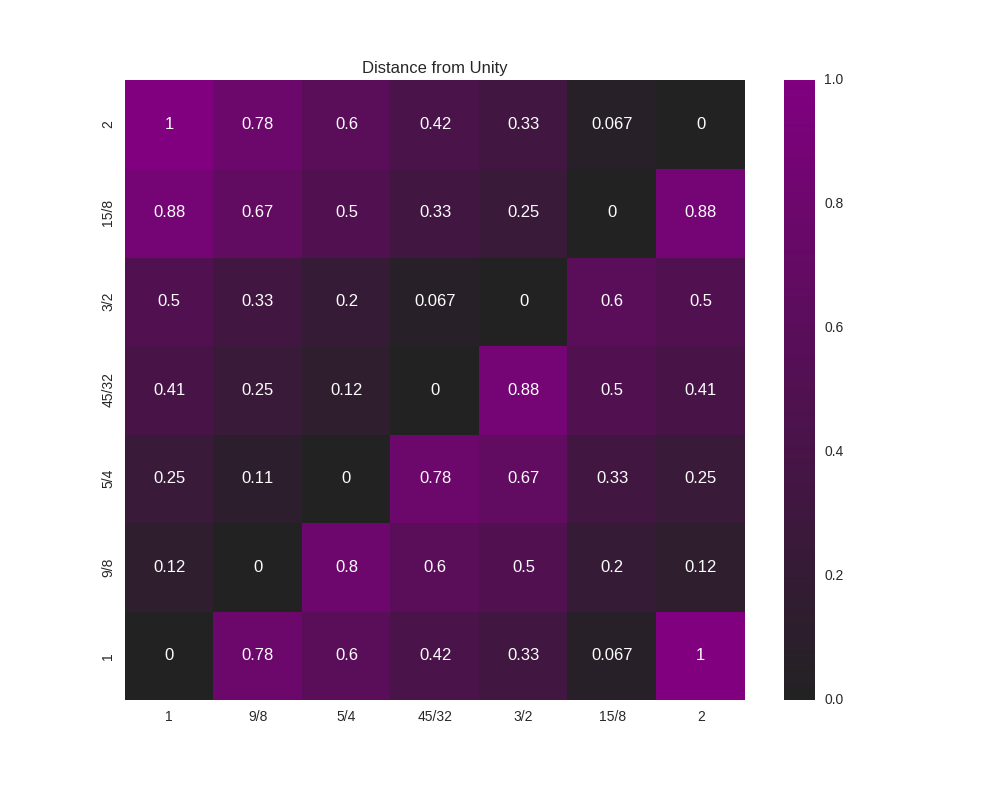
We could even do something like look for perfect fifths within our scale:

def metric_fifth(degree):
    p5 = sp.Rational(3,2)
    normalized_degree = normalize_interval(degree)
    y = normalize_interval(p5 / normalized_degree).evalf()
    y = y if y == 1 else 0
    return y

scale = create_euler_fokker_scale([3,5],[2,1])
matrix = consonance_matrix(scale, metric_function=metric_fifth,
  title="Relation to Perfect Fifth", annot=False)

which gives us:

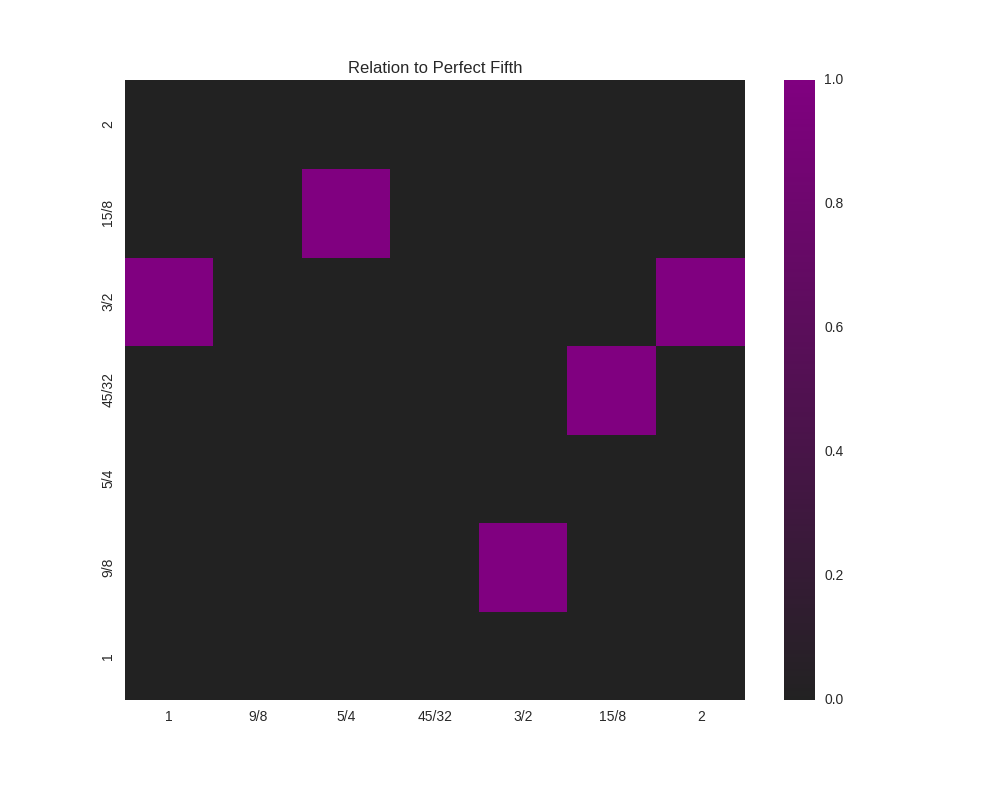
where the highlighted cells denote perfect fifths.

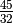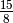You’ll note that the entry for $\frac{45}{32}$ and $\frac{15}{8}$ is 1 (a perfect fifth). We can verify this:

print(normalize_interval(sp.Rational(45,32)  / sp.Rational(15,8)))
3/2