Number Theory¶

While this part of the package isn’t particularly fleshed out yet, there are a few number-theoretic functions for the analysis of scales.

Odd Limits¶

PyTuning contains functions for finding the odd Limit for both intervals and scales.

We can define and interval – say, 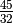$\frac{45}{32}$ , and fine its odd-limit with the following:

from pytuning.number_theory import odd_limit

interval = sp.Rational(45,32)
limit = odd_limit(interval)

which yields and answer of 45.

One can also find the odd limit of an entire scale with the find_odd_limit_for_scale() function:

from pytuning.scales import create_euler_fokker_scale
from pytuning.number_theory import find_odd_limit_for_scale

scale = create_euler_fokker_scale([3,5],[3,1])
limit = find_odd_limit_for_scale(scale)

which yields 135. (Examining the scale:

$\left [ 1, \quad \frac{135}{128}, \quad \frac{9}{8}, \quad \frac{5}{4}, \quad \frac{45}{32}, \quad \frac{3}{2}, \quad \frac{27}{16}, \quad \frac{15}{8}, \quad 2\right ]$

you will see that this is the largest odd number, and is found in the second degree.)

Prime Limits¶

One can also compute prime limits for both scales and intervals. Extending the above example, one would assume that the Euler-Fokker scale would have a prime-limit of 5, since that’s the highest prime used in the generation, and in fact:

from pytuning.scales import create_euler_fokker_scale
from pytuning.number_theory import find_prime_limit_for_scale

scale = create_euler_fokker_scale([3,5],[3,1])
limit = find_prime_limit_for_scale(scale)

will return 5 as the limit.