Scale Creation¶
There are several scale-creation functions in the package. They are found in
pytuning.scales and can be imported into the program’s namespace with
from pytuning.scales import *
(Note that for interactive use these are imported by default).
The Harmonic Scale¶
We’ll start with the harmonic scale; it will illustrate many of the concepts used in scale creation.
There are two important concepts to understand:
- Normalization: If a scale is normalized (which is the default in all cases), then the intervals of the scale are normalized to fall within a single octave. This means scaling the interval either up or down the number of octaves needed to make the interval fall between the unison and the octave.
- The Octave: Normally an octave is defined as a doubling of frequency (
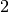 ),
but it is possible to define an octave by some other number. If this is the case
the normalization will takes place over this new octave.
),
but it is possible to define an octave by some other number. If this is the case
the normalization will takes place over this new octave.
The function to create a harmonic scale is, create_harmonic_scale:
-
pytuning.scales.create_harmonic_scale(first_harmonic, last_harmonic, normalize=True, octave=2)¶ Create a harmonic scale
Parameters: - first_harmonic – The first harmonic
- last_harmonic – The last harmonic
- normalize – If true, normalize the scale to an octave
(2/1 by default, otherwise taken from
octave) - octave – The definition of the formal octave.
Returns: The scale
As an example of use, a normalized scale constructed from harmonics 3 to 20:
scale = create_harmonic_scale(3,20)
which yields:
![\left [ 1, \frac{13}{12}, \frac{7}{6}, \frac{5}{4}, \frac{4}{3},
\frac{17}{12}, \frac{3}{2}, \frac{19}{12}, \frac{5}{3}, \frac{11}{6}, 2\right ]](_images/math/08125051c20ae13d2f12ec5a089c59f5b07bf226.png)
To create a non-normalized scale:
scale = create_harmonic_scale(3,10, normalize=False)
which yields:
![\left [ 1, \frac{4}{3}, \frac{5}{3}, 2, \frac{7}{3}, \frac{8}{3}, 3,
\frac{10}{3}\right ]](_images/math/7c290290b6a9f376e13bd524c33c7aff161f6953.png)
As an example, if we create a non-normalized harmonic scale of 10 harmonics:
harmonic_scale = create_harmonic_scale(1, 10, normalize=False)
We have the following scale:
![\left [ 1, \quad 2, \quad 3, \quad 4, \quad 5, \quad 6, \quad 7,
\quad 8, \quad 9, \quad 10\right ]](_images/math/653b645a313c6d3f5113b225dd373e51a2b95794.png)
If we normalize it each interval is scaled by a power of two to fall within 1
and 2. So, for example, the 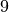 becomes
becomes  , because the
nine must be scaled by three octaves to fall within that range:
, because the
nine must be scaled by three octaves to fall within that range:
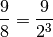
So the normalized scale is:
![\left [ 1, \quad \frac{9}{8}, \quad \frac{5}{4}, \quad
\frac{3}{2}, \quad \frac{7}{4}, \quad 2\right ]](_images/math/bd8501f05c501081ef5527f7493bc55b95aacf82.png)
But if we change our octave definition to be 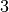 , we normalize on powers
of 3:
, we normalize on powers
of 3:
harmonic_scale = create_harmonic_scale(1, 10, octave=3)
yields:
![\left [ 1, \quad \frac{10}{9}, \quad \frac{4}{3}, \quad \frac{5}{3},
\quad 2, \quad \frac{7}{3}, \quad \frac{8}{3}, \quad 3\right ]](_images/math/8670c2d222cab19f2c98fd5df787a7efe8eef532.png)
Equal Divsion of the Octave (Equal Temprament)¶
Equal temperament scales can be created with the create_edo_scale()
function. Note that this function does not accept a normalize argument, because
EDO scales are normalized by definition. If does, however, allow you to change the
definition of the formal octave.
-
pytuning.scales.create_edo_scale(number_tones, octave=2)¶ Create an equal division of octave (EDO, ET) scale.
Parameters: - number_tones – The number of tones/divisions in the scale
- octave – The formal octave (frequency ratio)
Example, 12T-ET:
edo_scale = create_edo_scale(12)
will yield the normal equal-tempered scale used in western music:
![\left [ 1, \sqrt[12]{2}, \sqrt[6]{2}, \sqrt[4]{2}, \sqrt[3]{2}, 2^{\frac{5}{12}},
\sqrt{2}, 2^{\frac{7}{12}}, 2^{\frac{2}{3}}, 2^{\frac{3}{4}}, 2^{\frac{5}{6}},
2^{\frac{11}{12}}, 2\right ]](_images/math/6d6d0e2c18d73e5a3d3e2b4986d989043ac74f35.png)
Note that the length of the scale is 13, as both the unison and octave are included by convention.
It is also possible to have a non-2 formal octave. The code:
edo_scale = create_edo_scale(12,3)
will yield:
![\left [ 1, \sqrt[12]{3}, \sqrt[6]{3}, \sqrt[4]{3}, \sqrt[3]{3}, 3^{\frac{5}{12}},
\sqrt{3}, 3^{\frac{7}{12}}, 3^{\frac{2}{3}}, 3^{\frac{3}{4}}, 3^{\frac{5}{6}},
3^{\frac{11}{12}}, 3\right ]](_images/math/1d61d4a96a7a86d81ed6f930a20f36425f5da90c.png)
Scales from a Generator Interval¶
The create_equal_interval_scale() function will generate a scale from a
generator interval. This is the base function for several other scale types
(for example, the Pythagorean scale is created with a generator interval
of  ).
).
In he creation of a scale, the generator interval can either be used directly (for, for example, making each successive tone a generator interval above the previous tone), or in an inverted sense (making each interval a generator down from the previous). This function starts from the unison and walks down the number specified, walking up for the rest of the intervals.
-
pytuning.scales.create_equal_interval_scale(generator_interval, scale_size=12, number_down_intervals=6, epsilon=None, sort=True, octave=2, remove_duplicates=True, normalize=True)¶ Create a scale with equal-interval tuning
Parameters: - generator_interval – The interval to use for generation (
sympyvalue) - scale_size – The number of degrees in the scale
- number_down_intervals – The number of inverted intervals to use in scale construction.
- epsilon – Rounding parameter. If set to
Noneno rounding is done. Otherwise the scale degrees are rounded to the nearest epsilon - sort – If
True, sort the output by degree size - octave – The formal octave
- remove_duplicates – If
Trueremove duplicate entries - normalize – IF
True, normalize the degrees to the octave
In general one should keep epsilon at
Noneand perform and rounding outside the function.This is a base function from which several other scales are derived, including:
- The Pythagorean scale
A scale with a perfect fifth (3/2) as the generating interval
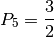
- The quarter-comma meantone scale
A scale in which the generating interval is a perfect fifth narrowed by one quarter of syntonic comma
![P_5 = \frac{\frac{3}{2}}{\sqrt[4]{\frac{81}{80}}}](_images/math/cd808b2cbf45c0725f57f0ab38601eb5559f6cd2.png)
- EDO Scales
EDO scales can be generated from an appropriate selection of the fifth. For example, the 12-TET scale would use the fifth:
![P_5 = \sqrt[\frac{7}{12}]{2}](_images/math/44474d0b92606c79d0c967bdb67259f5da815583.png)
- generator_interval – The interval to use for generation (
The Pythagorean Scale¶
This is the standard Pythagorean scale. Note that we can choose the number of up and down intervals in the scale. The default yields the standard scale, with the fourth degree as a diminished fifth, as opposed to the augmented fourth.
-
pytuning.scales.create_pythagorean_scale(scale_size=12, number_down_fifths=6, epsilon=None, sort=True, octave=2, remove_duplicates=True)¶ Create a Pythagorean scale
Parameters: - scale_size – The number of degrees in the scale
- number_down_fifths – The number of inverted fifths to use in scale construction.
- epsilon – Rounding parameter. If set to
Noneno rounding is done. Otherwise the scale degrees are rounded to the nearest epsilon - sort – If
True, sort the output by degree size - octave – The formal octave
- remove_duplicates – If
Trueremove duplicate entries
The Pythagorean scale is an even-interval scale with the following generating interval:
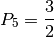
So, for the standard scale we can use:
scale = create_pythagorean_scale()
yielding:
![\left [ 1, \quad \frac{256}{243}, \quad \frac{9}{8}, \quad \frac{32}{27}, \quad
\frac{81}{64}, \quad \frac{4}{3}, \quad \frac{1024}{729},
\quad \frac{3}{2}, \quad \frac{128}{81}, \quad \frac{27}{16},
\quad \frac{16}{9}, \quad \frac{243}{128}, \quad 2\right ]](_images/math/62e515bea1990d47b6d70e34cb57a6f8410a4abe.png)
If we wanted the augmented fourth:
scale = create_pythagorean_scale(number_down_fifths=5)
yielding:
![\left [ 1, \quad \frac{256}{243}, \quad \frac{9}{8}, \quad \frac{32}{27},
\quad \frac{81}{64}, \quad \frac{4}{3}, \quad \frac{729}{512},
\quad \frac{3}{2}, \quad \frac{128}{81}, \quad \frac{27}{16},
\quad \frac{16}{9}, \quad \frac{243}{128}, \quad 2\right ]](_images/math/44664191964ebb9a0fb9cafbd363a06ba28008e4.png)
The Quarter-Comma Meantone Scale¶
-
pytuning.scales.create_quarter_comma_meantone_scale(scale_size=12, number_down_fifths=6, epsilon=None, sort=True, octave=2, remove_duplicates=True)¶ Create a quarter-comma meantone scale
Parameters: - scale_size – The number of degrees in the scale
- number_down_fifths – The number of inverted fifths to use in scale construction.
- epsilon – Rounding parameter. If set to
Noneno rounding is done. Otherwise the scale degrees are rounded to the nearest epsilon - sort – If
True, sort the output by degree size - octave – The formal octave
- remove_duplicates – If
Trueremove duplicate entries
The quarter-comma meantone scale is an even-interval scale with the following generating interval:
![P_5 = \frac{\frac{3}{2}}{\sqrt[4]{\frac{81}{80}}}](_images/math/cd808b2cbf45c0725f57f0ab38601eb5559f6cd2.png)
which is a perfect fifth (in a Pythagorean sense) narrowed by one quarter of the syntonic comma.
An example of use:
scale = create_quarter_comma_meantone_scale()
yields:
![\left [ 1, \quad \frac{8}{25} 5^{\frac{3}{4}}, \quad \frac{\sqrt{5}}{2},
\quad \frac{4 \sqrt[4]{5}}{5}, \quad \frac{5}{4}, \quad \frac{2}{5} 5^{\frac{3}{4}},
\quad \frac{16 \sqrt{5}}{25}, \quad \sqrt[4]{5},
\quad \frac{8}{5}, \quad \frac{5^{\frac{3}{4}}}{2},
\quad \frac{4 \sqrt{5}}{5}, \quad \frac{5 \sqrt[4]{5}}{4},
\quad 2\right ]](_images/math/45da4e5ed406331ccb3050b47c617411a2796a8d.png)
Euler-Fokker Genera¶
-
pytuning.scales.create_euler_fokker_scale(intervals, multiplicities, octave=2, normalize=True)¶ Create a scale in the Euler-Fokker Genera
Parameters: - intervals – The factors to use for the construction (usually prime numbers)
- multiplicities – The multiplicities of the factors (see below)
- octave – The formal octave
- normalize – If
True, normalize the intervals to the octave.
intervalsandmultiplicitiesshould both be lists of equal length. The entries inmultiplicitiesgive the number of each factor to use. Therefore the following:intervals = [3,5,7] multiplicities = [1,1,1] scale = create_euler_fokker_scale(intervals, multiplicities)
Will create a scale with one 3, one 5, and one 7 as generators.
The above will produce the following scale:
![\left [ 1, \frac{35}{32}, \frac{5}{4}, \frac{21}{16}, \frac{3}{2}, \frac{105}{64},
\frac{7}{4}, \frac{15}{8}, 2\right ]](_images/math/4550199eb6babfecda4751156031b41eacb0a216.png)
Also note that the two statements will generate the same output:
intervals = [3,5,7] multiplicities = [2,2,1] scale1 = create_euler_fokker_scale(intervals, multiplicities) intervals = [3,3,5,5,7] multiplicities = [1,1,1,1,1] scale2 = create_euler_fokker_scale(intervals, multiplicities) scale1 == scale2 True
Diatonic Scales¶
-
pytuning.scales.create_diatonic_scale(generators, specification)¶ Create a diatonic scale.
Parameters: - generators – The generator intervals (see below)
- specification – The scale specification. This is a list
of
charsthat correspond to entries in the generators. Note that if all the character representations are a single character, you can pass the specification in as a string for convenience.
Returns: The specified scale
generatorsis a list of tuples, the first member of which is an interval specification, the second of which is a character representation. The entries inspecificationshould correspond to this value.As an example, we can create the 12 EDO generators thus:
edo12_constructors = [ (sp.power.Pow(2,sp.Rational(2,12)), "T"), (sp.power.Pow(2,sp.Rational(1,12)), "s"), ]
We can then create the standard major mode with:
create_diatonic_scale(edo12_constructors, ["T","T","s","T","T","T","s"])
which will yield:
![\left [ 1, \quad \sqrt[6]{2}, \quad \sqrt[3]{2}, \quad 2^{\frac{5}{12}},
\quad 2^{\frac{7}{12}}, \quad 2^{\frac{3}{4}}, \quad 2^{\frac{11}{12}},
\quad 2\right ]](_images/math/e9ee490893c8dc36e0e2a79fc278509f7f26f4e6.png)
As another example of creating a diatonic scale, we can use the five-limit
constructors (which are defined in pytuning.constants):
five_limit_constructors = [
(sp.Rational(16,15), "s"),
(sp.Rational(10,9), "t"),
(sp.Rational(9,8), "T"),
]
to create Ptolemy’s Intense Diatonic Scale:
from pytuning.constants import five_limit_constructors
from pytuning.scales import create_diatonic_scale
scale = create_diatonic_scale(five_limit_constructors,
["T", "t", "s", "T", "t", "T", "s"])
which gives us:
![\left [ 1, \quad \frac{9}{8}, \quad \frac{5}{4}, \quad \frac{4}{3}, \quad
\frac{3}{2}, \quad \frac{5}{3}, \quad \frac{15}{8}, \quad 2\right ]](_images/math/f577ac1be5ac0b19d7dcc07ac3e9939b26316c83.png)
Note that if every identifier is a single-character string, specification
can also be passed in as a string. So this is equivalent:
from pytuning.constants import five_limit_constructors
from pytuning.scales import create_diatonic_scale
scale = create_diatonic_scale(five_limit_constructors, "TtsTtTs")