Utilities¶
The PyTuning package contains some utilities which may be useful. In general these tend to be smaller utilities and tasks that are useful in the analysis of musical scales, but they are not full-featured “things” in and of themselves.
Interval Normalization¶
-
pytuning.utilities.normalize_interval(interval, octave=2)¶ Normalize a musical interval
Parameters: - interval – The interval to normalize. Should be a frequency ratio, most usefully expressed as a sympy.Rational or related data item
- octave – The formal octave. Defaults to 2
Returns: The interval, normalized
Note that any formal octave can be used. In normal usage a 2 will be used (i.e., a doubling of frequency is an octave).
Normalization works by finding the smallest power of two (or
octave) that when multiplied by the interval (in the case of an interval less than 1) or divided into the interval (for intervals greater than 2) will bring the interval into the target range of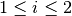 .
.
As an example, the interval 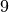 would normalize to
would normalize to 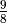 , because
9 needs to be scaled down by three octaves to fall within the limit of 1 and 2:
, because
9 needs to be scaled down by three octaves to fall within the limit of 1 and 2:
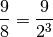
ni = normalize_interval(sp.Integer(9))
print(ni)
9/8
One can also normalize on a non-standard interval, for example, 3:
ni = normalize_interval(sp.Integer(34), octave=3)
print(ni)
34/27
Distinct Intervals¶
-
pytuning.utilities.distinct_intervals(scale)¶ Find the distinct intervals in a scale, including inversions
Parameters: scale – The scale to analyze Returns: A list of distinct intervals The scale should be specified as a list of
sympynumerical values (RationalorInteger). Note that the convention adopted in this code is that scale[0] is a unison and scale[-1] is the formal octave (often 2).As an example of a valid scale, a standardized Pythagorean tuning could be passed into the function:
![\left [ 1, \frac{256}{243}, \frac{9}{8}, \frac{32}{27},
\frac{81}{64}, \frac{4}{3}, \frac{1024}{729}, \frac{3}{2},
\frac{128}{81}, \frac{27}{16}, \frac{16}{9},
\frac{243}{128}, 2\right ]](_images/math/ac92c94cbeca780066ecc8f05ff3e2acde313642.png)
If one were hand-crafting this scale, it would look something like:
import sympy as sp scale = [sp.Integer(1), sp.Rational(256,243), sp.Rational(9,8), ...]
The function returns a list in rational/symbolic terms. If numerical values are needed, one can, for example, map
ratio_to_centsto obtain it:di = distinct_intervals(scale) di_in_cents = [ratio_to_cents(x) for x in di]
distinct_intervals() returns all the distinct intervals within a musical
scale. Note, though, that it does not include the unison (or the octave) in the
results, as all scales contain those intervals by definitions.
As an example, if we were to take a Pythagorean scale and find the intervals that exist within it:
pythag = create_pythagorean_scale()
di = distinct_intervals(pythag)
we end up with:
![\left [ \frac{2187}{2048}, \quad \frac{256}{243}, \quad \frac{8192}{6561}, \quad \frac{262144}{177147},
\quad \frac{4096}{2187}, \quad \frac{3}{2}, \quad \frac{243}{128}, \quad \frac{1024}{729},
\quad \frac{19683}{16384}, \quad \frac{729}{512},
\quad \frac{6561}{4096},
\quad \frac{65536}{59049}, \quad \frac{177147}{131072}, \quad \frac{59049}{32768}, \quad \frac{81}{64}, \quad
\frac{32}{27}, \quad \frac{27}{16},
\quad \frac{4}{3}, \quad \frac{9}{8}, \quad \frac{32768}{19683},
\quad \frac{16}{9}, \quad \frac{128}{81}\right ]](_images/math/666a72e94207c2ce81be71fc4906f8f3b952d614.png)
Converting a Ratio to a Cent Value¶
-
pytuning.utilities.ratio_to_cents(ratio)¶ Convert a scale degree to a cent value
Parameters: ratio – The scale degree ( sympyvalue)Returns: The scale degree in cents Calculates:
![\sqrt[2^{\left[ \frac{1}{1200} \right]}]{\text{degree}}](_images/math/76eab82a5a3f914f2a16757f28d853df7ef723c8.png)
Note that this function returns a floating point number, not a
sympyratio.
This function is useful if you have a symbolic value (a rational or transcendental, for example) and you want to see its value in cents (a logarithmic scale in which there are 1200 steps in a factor of two). For example:
interval = sp.Rational(3,2) # A perfect fifth
cents = ratio_to_cents(interval)
print(cents)
701.955000865387
Converting a Cent Value to a Ratio¶
-
pytuning.utilities.cents_to_ratio(cents)¶ Convert a cent value to a ratio
Parameters: cents – The degree value in cents Returns: the frequency ratio
This function takes a cent value and returns it as a frequency ratio (a
sympy floating point number).
print(cents_to_ratio(700.0))
1.49830707687668
(In other words, the 12-EDO fifth (700 cents) is very close to that of the
Pythagorean fifth ( , or 1.5).)
, or 1.5).)
Converting a Note Number to a Frequency¶
-
pytuning.utilities.note_number_to_freq(note, scale=None, reference_note=69, reference_frequency=440.0)¶ Convert a note number (MIDI) to a frequency (Hz).
Parameters: - note (reference) – The note number (0<=note<=127)
- scale – The scale. If none it assume EDO 12.
- note – The conversions reference note
- reference_frequency – The frequency of the reference note
Returns: The frequency of the note in Hertz
The default values for
reference_noteandreference_frequencycorrespond to standard orchestral tuning, a4 = 440 Hz.
With this function we can calculate the frequency of any note number. If defaults to the MIDI standard, which pegs note number 69 to 440 Hz and uses a 12-EDO scale.
As an example, MIDI note 60 (Middle-C):
print(note_number_to_freq(60))
261.625565300599
But if, for example, we wanted to use a different pitch standard, we could peg A to 444 Hz.
print(note_number_to_freq(60, reference_frequency=444.0))
264.003979530604
You can also pass in a non-EDO tuning if you’re converting a different kind of scale to frequencies. This is used often in the code associated with the tuning tables.
Naming A Ratio¶
-
pytuning.utilities.ratio_to_name(ratio)¶ Convert a scale degree to a name
Parameters: ratio – The input scale degree (a sympyvalue)Returns: The degree name if found, Noneotherwise
This function will look up the name of a ratio and return it (returning None)
if it is not found.
As an example:
pythag = create_pythagorean_scale()
names = [ratio_to_name(x) for x in pythag]
names now contains:
['Unison',
'Pythagorean Minor Second',
'Pythagorean Major Second',
'Pythagorean Minor Third',
'Pythagorean Major Third',
'Perfect Fourth',
'Pythagorean Diminished Fifth',
'Perfect Fifth',
'Pythagorean Minor Sixth',
'Pythagorean Major Sixth',
'Pythagorean Minor Seventh',
'Pythagorean Major Seventh',
'Octave']
There are currently about 260 intervals in the internal catalog, so while not complete, the database is fairly extensive.
Comparing Two Scales¶
-
pytuning.utilities.compare_two_scales(scale1, scale2, reference_freq=220.0, title=['Scale1', 'Scale2'])¶ Compare two scales
param scale1: The first scale (list of sympyvalues)param scale2: The second scale (list of sympyvalues)param reference_freq: The frequency (Hz) of the first degree param title: The scale names (list of strings with len = 2) returns: None, (ie nothing)
This function will produce a simple textual representation of the difference between two scales. As an example, comparing the 12-EDO and Pythagorean scales:
from pytuning.scales import create_edo_scale, create_pythagorean_scale
from pytuning.utilities import compare_two_scales
scale_1 = create_edo_scale(12)
scale_2 = create_pythagorean_scale()
compare_two_scales(scale_1, scale_2, title=['12-TET', 'Pythagorean'])
produces:
12-TET Pythagorean
Cents Freq Cents Freq Delta(Cents)
========= ========= ========= ========= ============
0.0000 220.0000 0.0000 220.0000 0.0000
100.0000 233.0819 90.2250 231.7695 9.7750
200.0000 246.9417 203.9100 247.5000 -3.9100
300.0000 261.6256 294.1350 260.7407 5.8650
400.0000 277.1826 407.8200 278.4375 -7.8200
500.0000 293.6648 498.0450 293.3333 1.9550
600.0000 311.1270 588.2700 309.0261 11.7300
700.0000 329.6276 701.9550 330.0000 -1.9550
800.0000 349.2282 792.1800 347.6543 7.8200
900.0000 369.9944 905.8650 371.2500 -5.8650
1000.0000 391.9954 996.0900 391.1111 3.9100
1100.0000 415.3047 1109.7750 417.6562 -9.7750
1200.0000 440.0000 1200.0000 440.0000 0.0000