Scale Analysis and Creation (Redux)¶
Scale Creation describes the way that many standard scales are generated from within the package. But there are other ways to create scales.
Mode Selection¶
When one creates a scale – for example, the Pythagorean scale or a scale of the Euler-Fokker Genera – one can looks at the various modes that can be created for that scale and evaluate them by certain criteria.
The find_best_modes() function can be used for this. This function accepts
and input scale, the number of tones for the mode, and the optimization functions
that should be used for evaluating the scale.
As an example, one scale that’s I’ve used in compositions is created from choosing
a seven-note mode from a harmonic scale, optimized over the metric sum_p_q_for_all_intervals().
This particular scale is based upon the harmonic series referenced to the fourth
harmonic.
The following code:
harmonic_scale = create_harmonic_scale(4,30)
modes = find_best_modes(harmonic_scale,
num_tones=7,
sort_order = ['sum_p_q_for_all_intervals'],
num_scales=1,
metric_function = sum_p_q_for_all_intervals)
yields the following object:
[{'mask': (0, 2, 4, 5, 8, 12, 14, 15),
'original_scale': [1,
17/16,
9/8,
19/16,
5/4,
21/16,
11/8,
23/16,
3/2,
25/16,
13/8,
27/16,
7/4,
29/16,
15/8,
2],
'scale': [1, 9/8, 5/4, 21/16, 3/2, 7/4, 15/8, 2],
'steps': [2, 2, 1, 3, 4, 2, 1],
'sum_p_q_for_all_intervals': 572}]
The returned scale:
![\left [ 1, \quad \frac{9}{8}, \quad \frac{5}{4},
\quad \frac{21}{16}, \quad \frac{3}{2},
\quad \frac{7}{4}, \quad \frac{15}{8}, \quad 2\right ]](_images/math/318a24c4813fa279afe47894151d68c3e8c7676a.png)
minimizes the metric for all possible combinations of 7 notes chosen from the original harmonic scale.
Factoring an Interval¶
Sometimes it is interesting to take an interval and find an expression for that
interval over some set of generator intervals. For this the function
find_factors() is provided.
One has to specify the generator intervals. This is done by passing the function
a list of tuples. Each tuple has two members: The generator interval, and a
character representation of the generator interval. Usually these are a single,
unique character (such as X), but it can also be in the form 1/X. If it
is in this form the generator interval should be the reciprocal of the interval
designated by X.
As an example, we could create a generator interval that represents the tone and semi-tone of a 31-EDO scale:
edo31_constructors = [
(sp.power.Pow(2,sp.Rational(2,31)), "T"), # a tone
(sp.power.Pow(2,sp.Rational(1,31)), "s"), # a semitone
]
(Note that the tone is just twice the semitone, so we could probably get by with just defining the semitone).
Now we can define an interval, say, one of the intervals of the Pythagorean
scale:
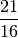
and see what factoring yields an interval closest to the original.
results = find_factors(interval, edo31_constructors)
results
results now contains the factoring, the factoring in symbolic terms, and
the resultant interval.
([2**(2/31), 2**(2/31), 2**(2/31), 2**(2/31), 2**(2/31), 2**(2/31)],
['T', 'T', 'T', 'T', 'T', 'T'],
2**(12/31))
The last entry is the returned interval:
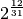
If one is interested in seeing how closely the factored interval matches the
original interval, the ratio_to_cents() function in pytuning.utiities can
be used.
from pytuning.utilities import ratio_to_cents
print(ratio_to_cents(results[2] / interval))
yields:
-6.26477830225428
In other words, the derived interval is flat about 6.3 cents from the target interval.
Approximating a Scale with Another Scale¶
The above factoring of an interval over a set of generators can be extended: a scale can be factored too.
To do this the create_scale_from_scale() function is used.
The first step in using this function is to create an interval function. It is
similar to find_factors() in that it accepts an interval and a max factor, and
it returns the factor. But the actual generator intervals are bound to this function.
The easiest way of creating this function is to take the generator intervals
that you’re interested in and to bind them to find_factors() via a partial
function application. As an example, we can take the five-limit constructors:
five_limit_constructors = [
(sp.Rational(16,15), "s"),
(sp.Rational(10,9), "t"),
(sp.Rational(9,8), "T"),
]
And use them to approximate the Pythagorean scale:
from pytuning.scales import create_pythagorean_scale
from pytuning.scale_creation import create_scale_from_scale, find_factors
from pytuning.constants import five_limit_constructors
from functools import partial
interval_function = partial(find_factors, constructors=five_limit_constructors)
pythag = create_pythagorean_scale()
results = create_scale_from_scale(pythag, interval_function)
The return value is a tuple, the first element of which is derived scale, the second of which is the symbolic factoring. The scale which was found was
![\left [ 1, \quad \frac{16}{15}, \quad \frac{9}{8}, \quad \frac{32}{27},
\quad \frac{81}{64}, \quad \frac{4}{3}, \quad \frac{1024}{729},
\quad \frac{3}{2}, \quad \frac{128}{81}, \quad \frac{27}{16},
\quad \frac{16}{9}, \quad \frac{243}{128}, \quad 2\right ]](_images/math/d53287a8fbb7990c0f09413922c256828f6a8b9b.png)
If you look at the Pythagorean scale:
![\left [ 1, \quad \frac{256}{243}, \quad \frac{9}{8}, \quad
\frac{32}{27}, \quad \frac{81}{64}, \quad \frac{4}{3},
\quad \frac{1024}{729}, \quad \frac{3}{2},
\quad \frac{128}{81}, \quad \frac{27}{16},
\quad \frac{16}{9}, \quad \frac{243}{128}, \quad 2\right ]](_images/math/08e1276f37fca319bab289ced30d414f552f4cc4.png)
you can see that they only differ in the second degree (which if we look at the first member of the return we can see is factored as [‘s’]). Looking at how much they differ:
ratio = results[0][1] / pythag[1]
print(ratio)
81/80
print(ratio_to_name(ratio))
Syntonic Comma
delta = ratio_to_cents(ratio)
print(delta)
21.5062895967149
we see that the difference is 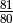 , which is the syntonic comma
(about 21.5 cents).
, which is the syntonic comma
(about 21.5 cents).
create_scale_from_scale() can also accept a tone_table which is a list
of the potential breakdowns that can be used in the analysis.
Note that the first entry of the factors is always for the ratio 1, and is returned as an empty list (as there really are no factors in this sense).